Chapter 5: Complete Guide To Gases
- Mayya Alocci
- Oct 26, 2023
- 4 min read
Gas Pressure and Its Measurement
Gases have no fixed shape or volume. The variables that describe gases include:
Pressure(P), Volume(V), Temperature(T) and Moles(n).
Pressure can be measured in atm (atmospheres), torr, mmHg, or Pa (pascals).
1 atm = 760 torr = 760 mmHg
Volume can be measured in ml (milliliters) or L (liters).
Temperature must be converted to Kelvin for all the gas equations.
T=°C+273.15 = K
Gas Laws
Combined Gas Law

where P1= initial Pressure, V1 = initial volume, T1 = initial temperature
P2 = final pressure V2 = final volume T2 =final temperature
Let's not forget that temperature needs to be in Kelvin.
Combined gas law will be used when a property is changing. For example, the question is stating that the initial volume has doubled and asking what will the new pressure be.
Combined gas law can also be converted into other gas laws.
When temperature is constant, we get P1V1 = P2 V2 (Boyle's Law)
When pressure is constant, we get V1/T1 = V2 /T2 (Charles’s law)
Practice: A volume of air occupying 12.0 dm3 at 98.9 kPa is com- pressed to a pressure of 119.0 kPa. The temperature remains constant. What is the new volume?
Let's first write out what we are given.
P1=98.9 kPa
V1=12.0 dm3
P2 =119.0 kPa
V2 =?
Since temperature is constant, the equation becomes P1V1= P2 V2
Plugging in, we get 98.9 kPa*12.0 dm3 = 119.0 kPa*V2
V2 = 9.97 dm3
Remember: The volume of 1 mole of gas at STP (standard temperature and pressure 0°C and 1 atm pressure) is 22.4L
The Ideal Gas Law
The ideal gas law is
PV =nRT
where P is pressure in the units of atm
V is volume in units of L
n is the number of moles of gas
R is the ideal gas constant 0.0821 L*atm/(K*mol)
T is temperature in K
Ideal gas law is used when we are given a set of conditions and looking for an unknown. For example, we are given temperature, moles and pressure and are looking for volume.
Practice: How many grams of oxygen, O2 , are there in a 50.0-L gas cylinder at 21°C when the oxygen pressure is 15.7 atm?
Let's write out the given
P = 15.7 atm
V= 50.0L
n = ?
T= 21°C+273 = 294 K
PV =nRT
15.7 atm*50.0L = n(0.0821 L*atm/(K*mol))(294 K)
n = 32.5 mol
We are asked for grams and need to convert moles to grams using the molar mass
32.5 mol (32gO2/1molO2) = 1.04 * 10^2 g O2
Gas Density and Molecular Mass
(P)MM=dRT is an equation that allows to find density from molar mass or molar mass from density.
P is pressure in atm
MM is molar mass in g/mol
d is density in g/L
R is the ideal gas constant 0.0821 L*atm/(K*mol)
T is temperature in K
Example: At 2.60*10°C, the density of geraniol is 0.480 g/L at a pressure of 103 torr. What is the molecular mass of geraniol?
Let's write out what is given.
d = 0.480 g/L
P = 103 torr /760 = 0.135526 atm
T = 2.60*10°C+273.15 = 533.15K
Now, we can plug everything in:
0.135526 atm (MM) = 0.480 g/L*0.0821 L*atm/(K*mol)*533.15K
MM= 155g/mol
Stoichiometry Problems Involving Gas Volumes
We can use ideal gas law to find moles of gas if pressure and volume are given. We can then use moles in stoichiometry problems and calculations.
Gas Mixtures; Law of Partial Pressures
Dalton’s law of partial pressures states that the sum of the partial pressures of all the different gases in a mixture is equal to the total pressure of the mixture.
P total = Pa+Pb+...
Pa = XaPtotal where Xa is the mole fraction of a
Xa = moles of a/total moles
Practice: A mixture of gases contains 4.46 mol of neon (Ne), 0.74mol of argon (Ar), and 2.15 mol of xenon (Xe). Calculate the partial pressure of argon if the total pressure is 2.00atm.
Pargon= Xargon (Ptotal)
Xargon = nargon/(nneon+nargon+nxenon) = 0.74mol/(4.46mol+0.74mol+2.15mol) = 0.10068
Pargon= 0.10068(2.00atm) = 0.20atm
Kinetic Theory of an Ideal Gas
The kinetic theory of ideal gas has five postulates.
The volume occupied by gas particles is negligible.
Molecules move randomly in straight line motion.
The forces of attraction or repulsion between gas molecules are negligible except when they collide
When gas molecules collide with one another no energy is lost
The average kinetic energy of a molecule is proportional to the absolute temperature.
Molecular Speeds; Diffusion and Effusion
We can calculate the average molecular speed of gas using root-mean-square (rms) molecular speed equation.
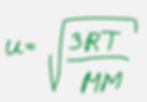
Where u is the room mean square speed
R is the ideal gas constant 8.31 kg*m2/(s^2*K*mol)
T is temperature in K
MM is the molar mass in kg/mol
Example: Calculate the rms speed of O2 molecules in a cylinder at 21°C and 15.7 atm.
Molar mass of O2 is 32g/mol but we need to convert it to kg/mol by diving by 1000.
We get 32*10^-3 kg/mol
T =21°C+273 = 294K
u=(3*8.31 kg*m2/(s^2*K*mol)*294K)/(32*10^-3 kg/mol) = 479 m/s
Let's now go over effusion versus diffusion.
Effusion:The process in which a gas flows through a small hole in a container
Diffusion: The process whereby a gas spreads out through another gas to occupy the space uniformly.
Rate of effusion is inversely proportional to the molar mass of the molecule.
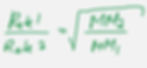
Example: Calculate the ratio of effusion rates of molecules of carbon dioxide, CO2, and sulfur dioxide, SO2, from the same container and at the same temperature and pressure.
First, lets get the molar masses for both compounds.
MM SO2 = 64.1g/mol
MM CO2 = 44.0g/mol
Rate CO2/Rate SO2 = √(64.1g/mol/44.0g/mol)= 1.21
Learn Chemistry with our Online Chemistry Tutor to ace your general chemistry class!
